Some Points on Plausible Reasoning
Today, it is typical for people to assert their opinions with tremendous self-assurance. The opinions that are held and asserted with an inordinate degree of confidence, however, are of a special kind, for they are ones that agree with the predominant cultural viewpoint - or what I will refer to as the cultural orthodoxy. The increasing erosion of the right to free speech is grounded in the confidence that the culturally orthodox position on the important moral and political issues is unquestionably true.
The only reason this view prevails today is that very few understand the fundamentals of human reasoning, which is on one level a mixture of deductive and inductive reasoning; on another level, human reasoning is fundamentally a matter of plausible reasoning, which is really a way of managing data that is less than certain. When we understand how plausible reasoning works, even on a rudimentary level, it becomes evident that the epistemic overconfidence that is typical today, especially among the young, is completely unwarranted and even dangerous.
Deduction
Plausible reasoning works with data, some of which is established fact, and some of which is the result of both deductive and inductive inference. What distinguishes deductive from inductive reasoning is that in the former, the conclusion is contained in the given premises, while in the latter (inductive reasoning), the conclusion is not; rather, the conclusion is the result of a jump or leap-we speak of jumping to conclusions. As an example of a simple deductive argument, consider the following:
All the marbles from urn A are red
The marble in my hand is from urn A
Therefore, the marble in my hand is red
Assuming that the data is correct, the conclusion follows necessarily from the information contained in the first two premises. Consider, too, the following:
If you come down with the flu, then you will have a fever
After taking your temperature, the doctor declares that you do not have a fever
Therefore, it follows that you do not have the flu
Again, all the information that allows us to assert rather conclusively that you do not have the flu is contained in the data provided.
Consider as well the following example of a basic deduction involving a hypothetical syllogism:
If I come down with the flu, then I won't be going to school tomorrow.
If I don't go to school tomorrow, then I will miss the final exam.
Therefore, if I come down with the flu, then I will miss the final exam.
Once again, the conclusion is contained in the data provided by the first two premises; all we are doing here is "educing" or drawing out the necessary implications of the data. If we were to add a new piece of data, such as "I did not miss the exam", then it would necessarily follow that "I went to school", and if I went to school, then "I did not come down with the flu".
Let us enlarge the set of data and attempt a more elaborate puzzle. Consider the following set of data:
Roha, Ariba, and Saad are very devout Muslims who faithfully observe Salat (daily prayer) every day, regardless of where they are. Roha generally does not use the subha (prayer beads) on Thursdays, and without the struggles with writing that affect some of her friends, writes some of the finest poetry in the school. Saad, who suffers from migraines, will always recite subha on Mondays, and is not known for his eloquent speeches. The person with a gift for eloquent speaking always recites subha on Thursdays.
There is enough information or data contained in the set above to work out which student has which gift, and which day of the week they can be found reciting subha, and what difficulties they struggle with.
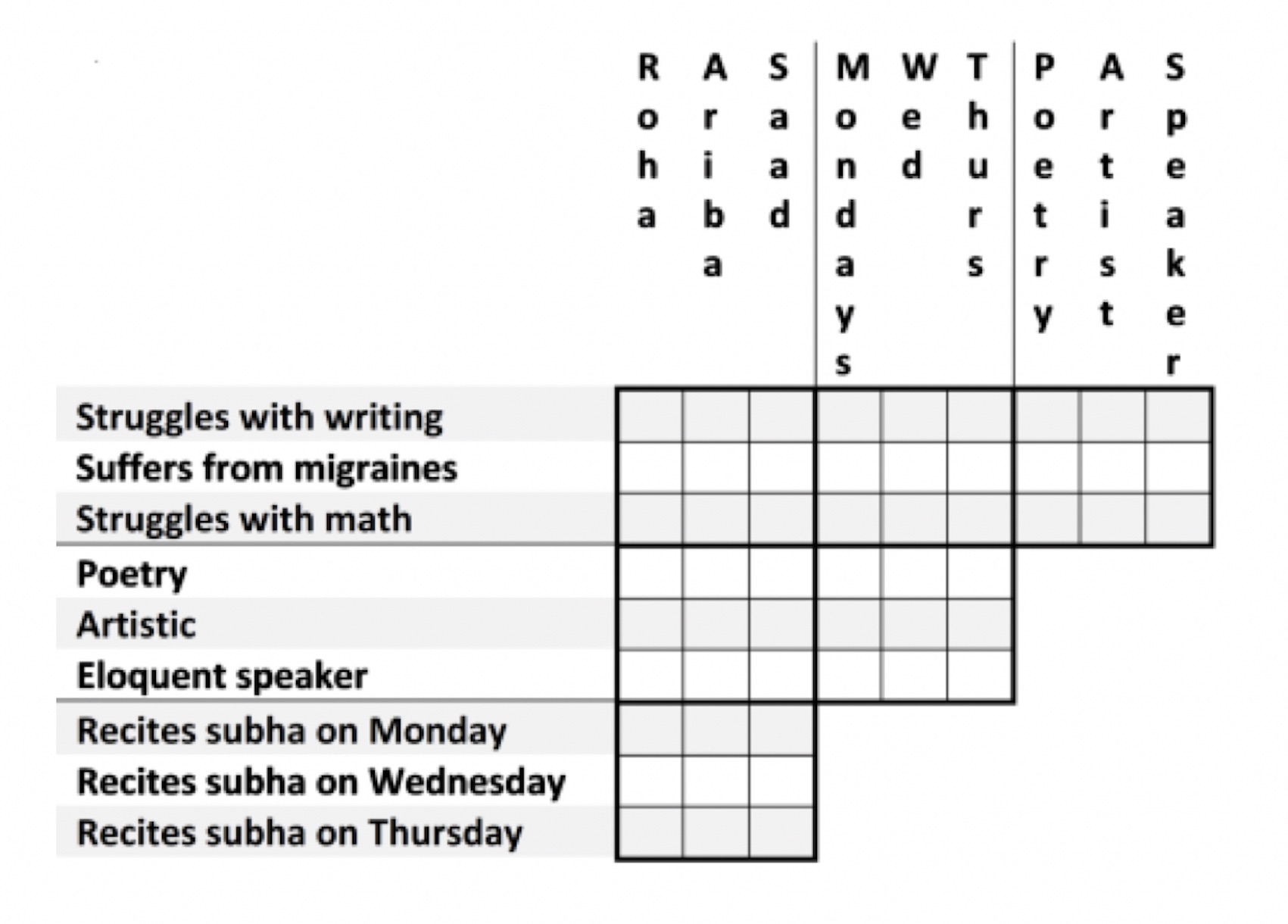
The above is a relatively simple puzzle, and working it out is a matter of simple deduction. We know that Roha does not use her prayer beads on Thursdays nor does she struggle with writing; rather, she writes the finest poetry. So under her column we can place an X beside "Struggles with writing" and an X beside "Recites subha on Thursday." We can also place an X, under her column, beside "Artistic" and "Eloquent speaker", and place an O beside Poetry - which allows us to place an X beside "Poetry" under Ariba and Saad's name. Saad suffers from migraines, so in his column we can place an X beside "Struggles with writing" and "Struggles with math", and an O beside "Suffers from migraines". This allows us to place an X beside "Suffers from migraines" under Ariba and Roha's name. This in turn allows us to see that Roha struggles with math and Ariba struggles with writing.
We can also place an X, in Saad's column, beside "subha on Wednesday" and "subha on Thursday", and an O beside Monday. That permits us to place an X under Roha and Ariba's name in the Monday row. Doing so allows us to see that Roha recites subha on Wednesday, which leaves Ariba as the one who recites on Thursday. Since the one with the gift of eloquent speaking recites subha on Thursdays, we know that Ariba is the fine speaker, which leaves Saad as the artistic student.
Puzzles such as these can become much more challenging (see end note), but even with more challenging puzzles, the information required to solve them is contained in the data either explicitly or implicitly. What is particularly interesting about deduction is that much of the information is implicit, and it takes some serious effort to make it explicit; doing so opens up avenues that permit us to make other pieces of implicit information explicit as well.
Most people tend to find such difficult puzzles far too taxing and will not make the effort, but completing such puzzles, that is, determining who has what gift and what deficiency, etc., or with respect to the more difficult puzzle below, who has the fastest pitch and which student represents which school is, although relatively difficult for most people, is still rather insignificant. Consider that in this world there are matters far more serious, such as moral, economic, or political matters. Moreover, the data regarding such moral, economic, or political matters is, in many cases, available (such as general principles and patterns), which means it is possible to make important points explicit through a process of deduction, points that are implicit in the explicitly known data. Many of us, however, are unaware of such basic and important moral, economic, or political implications of the available data because we are very often unwilling to make the effort required to draw out the logical implications of the data that we possess explicitly. This is especially true with regard to moral matters, because there are certain conclusions bearing on certain issues that many of us would like to be false, or beyond resolution.
Plausibility and Systematicity
What is interesting about such logical puzzles, especially the more difficult ones, is that each piece of data fits into a larger whole, very much like the pieces of a jigsaw puzzle. In the correct and completed product, there are no gaps or incongruities; all the needed parts are integrated into a unity. The correctly completed puzzle is also cohesive, that is, each piece of data is connected to other pieces of data; for if some piece of data is out of place, that is, assigned to the wrong place, then other pieces of available data will be affected and the whole puzzle will lack consistency and coherence; thus, the completed puzzle would not fit the entire set of given data (clues provided); a number of inconsistencies result, and so the puzzle in the end lacks harmony, elegance, and congruity. To see this, all we have to do is pay attention to what happens when we complete the puzzle and discover there are errors - what we discover are conflicts.
These properties, namely, completeness, inclusivity, unity and integrity, cohesiveness and coherence, functional simplicity and economy, elegance, symmetry, consistency and coordination of parts, etc., are the properties of the correctly completed puzzle, that is, logically consistent data ordered according to the information provided. These properties are the parameters of systematicity: a puzzle is like a system with many parts unified into a functional and coherent whole.
The most important point I wish to make, however, is that in the real world, we rarely, if ever, have complete and reliable information. In that light, consider how much more difficult such a logical puzzle would be to complete if the information available was not entirely reliable, that is, to some degree uncertain, only plausible (minimally, moderately, or highly). Like a chain, our conclusion would only be as strong as our weakest piece of data (i.e., our weakest link).
Consider too how much more difficult the puzzle would have been to solve had the information been overabundant; for example, if we were informed that Saad, who suffers from migraines and has failed math twice, sometimes recites subha on Mondays and Thursdays and won a public speaking contest a few years ago, and the person with a gift for eloquent speaking recites subha on Wednesdays and Thursdays, etc., we would have a much more difficult time determining who's who. In other words, an overabundance of information makes matters more difficult because, ultimately, we find ourselves in the position of needing further information to resolve conflicts that inevitably arise. Hence, an overabundance of information in the end amounts to a lack of information needed in order to fit each part into a coherent and cohesive whole.
This is the reason why deductive puzzles like the one above - or the more difficult one below in the end note - can take a half hour or so complete, but knowledge from the predominantly inductive sciences (i.e., chemistry, physics, biology, astronomy, etc.) takes centuries to develop and are never complete. Deductive reasoning is relatively simple because all the information needed to derive an absolutely certain conclusion is contained in the premises. Hence, the conclusion is determined, certain, that is, it necessarily follows from the given premises.
Inductive reasoning is not so simple, because the conclusion of an inductive argument is "information transcending". This means that the conclusion is not contained in the data provided by the premises - it "transcends" the data, or goes beyond the available information, that is, makes assertions that are inconclusive and possibly false. Inductive reasoning involves "jumping" to a conclusion, and the goal of inductive reasoning is to estimate the most reasonable jump, that is, to discover the most fitting estimate. For example,
20% of the marbles in this cup (sample), scooped from urn B, are green and 80% are red.
Therefore, 20% of all the marbles in urn B are green while the rest are red.
The conclusion, of course, is not necessarily true, but only probably so; for we went from the data contained in a sample to a conclusion about the whole. The conclusion is reasonably probable on condition that the sample in the cup is large enough and that the marbles in the urn have been well distributed. If the sample is small and the marbles have not been well distributed (mixed), then it is unrepresentative and is likely to be false; it may turn out that 45% of the marbles in urn B are green, etc.
Consider as well the following puzzle:
A carrot, a pile of pebbles, and a pipe made from a cob of corn are lying together in the middle of a field. (Our task is to estimate why that is the case). The difference between this puzzle and the two previous deductive puzzles is that here we are beginning with facts in evidence and proceeding to infer the reasons for the facts (the antecedent, prior conditions or causes that account for the facts in evidence). Instead of the luxury of a conditional thesis, such as "if he has the flu, then he will have a fever", all we know is that he has a fever and it is up to us to determine why - and of course there are a number of candidates (possible hypotheses). There are very often a number of possibilities that can explain any piece of evidence, but not all are equally fitting. One rather striking explanation for the carrot, pebbles and pipe lying together in a field is that during the winter, on that very spot, someone had built a snowman using a carrot for a nose, a pipe, and pebbles for the eyes and mouth. Although such an estimate is fitting, it lacks the force of deductive necessity - it is inconclusive; thus it has only a degree of plausibility. If the field were in Florida, this explanation would lack plausibility, but if the field is not a carrot field but perhaps a park located in a state or province that typically has lots of snow during the winter months, and plenty of children around, the inference that a snowman once stood here becomes much more plausible.
Our day to day reasoning is a matter of plausible reasoning, which is a combination of both deductive and inductive argumentation. A large part of the set of data available to us, possibly the most part, is made up of theses or propositions that are not established facts, but which have only a degree of plausibility - either minimal plausibility (.2), moderate plausibility (.5), or a rather high degree of plausibility (.8 or .9). Moreover, our data base is always incomplete - and even if this were not the case, how would we know it? And that is the fundamental reason why it is very difficult to know whether many of the conclusions we draw are absolutely or only putatively true, for an argument is only as strong as its weakest link. What is putatively true will be that set of data-out of a number of other sets of data - that has maximal plausibility. Whereas some subsets of data had to discard highly plausible data in order to maintain logical consistency, the maximally plausible and consistent set of data is, at least for the moment, true, or at least putatively so.
In order to demonstrate in very simple terms how this works, let us limit ourselves to three pieces of data. Using the two variables p and q to stand for the following two separate propositions: Saad struggles with math (p), and Roha struggles with math (p), and ~ which is the symbol for negation, we have the following set:
{~p, ~q, p v q}
This is translated as:
~p = Saad does not struggle with math (which, on the basis of our background knowledge, we will say is highly plausible, or .9)
~q = Roha does not struggle with math; (which we will say is minimally plausible, or .2)
p v q = Either Saad struggles with math or Roha struggles with math; (which is a highly plausible thesis, or .9)
Each piece of data is plausible on its own, but as a set of data, it is logically inconsistent. In other words, it is not possible that "Either Saad struggles with math or Roha struggles with math" is true, if it is also true that "Saad does not struggle with math" and "Roha does not struggle with math". And so this state of affairs demands that we restore consistency, and we can only do that by discarding a piece of data. This gives us three possible alternatives:
1. We can abandon p v q: "Either Saad struggles with math or Roha struggles with math", which is a highly plausible thesis (.9). In doing so, we are left with the following subset (S1): {Saad does not struggle with math, Roha does not struggle with math}.
2. We can abandon ~p: "Saad does not struggle with math", which is also a piece of data with high plausibility (.9), and this leaves us with the following subset (S2): {Roha does not struggle with math, either Saad struggles with math or Roha struggles with math}. Again, the discarded data is one of high plausibility (.9).
3. Finally, we can abandon ~q: "Roha does not struggle with math", which is minimally plausible (.2), and this leaves us with the following subset of data (S3): {Saad does not struggle with math, either Saad struggles with math or Roha struggles with math}. In this case, the discarded data is minimally plausible (.2).
The first alternative, S1, contains one piece of highly plausible data (.9) and one piece of minimally plausible data (.2), but the price for this subset is the loss of a highly plausible thesis (.9). The second alternative, S2, also contains one piece of highly plausible data (.9) and one piece of minimally plausible data (.2), but it too incurs a heavy loss, the dismissal of a highly plausible thesis (.9). The third alternative, S3, manages to discard minimally plausible data and keep two pieces of highly plausible data.
All three subsets (S1, S2, and S3) are consistent, but S3 is maximally plausible. From this set of data, we can conclude that since either Saad struggles with math or Roha struggles with math, and it is almost certain that Saad does not struggle with math, it follows that it is highly plausible that Roha struggles with math. And of course, this is consistent with our background knowledge of Roha and Saad, for example, Saad loves physics, but Roha loves literature, and it is unlikely that Saad would love physics if he struggled with math; moreover, Roha avoided courses that require math prerequisites, which might suggest that math is not her strong point. Of course, it is entirely possible that new data could upset the plausibility index of this conclusion - we might learn that Saad would like to study physics but is unrealistic about his intellectual abilities and that Roha is so mathematically adept that she finds the subject unchallenging and boring, etc.
A correctly resolved logical problem has the properties of completeness, inclusivity, unity and integrity, cohesiveness and coherence, functional simplicity and economy, elegance, symmetry, consistency and coordination of parts, etc., but it is these very properties that are the criteria for resolving a problem that is a matter of plausible reasoning, that is, when our goal is a matter of determining the best or maximally plausible estimate. Hence, the most plausible set of data (out of which our current estimate is constituted) will be that which is most complete, inclusive, integral, cohesive and coherent, the most functionally simple and elegant, etc.
Logical puzzles of a deductive nature, such as one of the two featured in this article, are contrived. Data is carefully selected and other data left out precisely in order to make possible a definitive conclusion. The real world, however, is just not like that; reality is far more complex. Data that is at our disposal is typically overabundant and inconsistent, and the data needed to resolve an impasse is often missing. Moreover, the data we have at our disposal is rarely "established fact", but is for the most part only minimally or moderately plausible. Hence, the best we can hope for is a best estimate that is putatively true, not definitively so.
Concluding Thoughts
When a conclusion of an argument makes sense to us, that is, when it is coherent, we have a tendency to assume that we have, as it were, a completed puzzle on our hands, a conclusion that enjoys the force of deductive necessity and that what we see is all there is to see. But like the piece of data that fits with two or three other pieces of data but does not fit into the larger context of ten or more pieces of data (as in a typical logical puzzle of the more challenging kind), what we see is not all there is. Although all that is true "makes sense", it is not the case that "all that makes sense is true" (i.e., all humans are animals, but not all animals are humans). With the introduction or discovery of new data, it often happens that what was earlier our best estimate is now relegated to a much lesser degree of plausibility and what was earlier estimated to be far less plausible becomes maximally so. What "makes sense" in a very limited context is often discovered to be inconsistent and incoherent in a larger context. In other words, in time we often discover that what we thought was "true" and complete is far from it. New information reveals that this or that piece of data has been improperly placed, that "this" or "that" is not the case, and that the world outside the mind is far more complex than we initially realized.
The problem with some writers, i.e., political pundits on the left and right, very conservative theologians, religious or political fundamentalists, etc., is not so much the conclusions that are logically drawn from their pool of rational data; rather, it is that the circle of data from which conclusions are educed is profoundly limited. Very often what is deduced from the principles they work with is indisputable, but the circle of data is too limited to guarantee anything more than a truth candidate, and it is precisely this "sense of incomplete information" that seems to be lacking today. Without an empirical orientation - as opposed to the idealist one - we tend not to suspect that our storehouse of data might very well be significantly incomplete. Hence, the epistemic overconfidence with which most people make assertions. All our ideas are derived from the world of experience - for nothing is in the intellect that was not first in the senses (peripatetic axiom). Indeed, our ideas are universal, but they are nonetheless limited by the effects of matter, that is, sense perception and our dependence upon observation of a thing's activity in order to grasp the natures of things - and things always act in time. It is only gradually, in time, that our information base is enlarged, and so we always seem to be in a position to revise the plausibility index of some of our data and rethink the beliefs we previously held. If this rarely happens today, it is only because thinking takes effort and patience, and many lack the patience required to "suspend disbelief" and the willingness to expend one's energy thinking, listening, reasoning, and revising.
End Notes
1. The five high school baseball players who appear in this puzzle all represent different schools. All the information needed to work out which school each player represents and his fastest pitch to date is contained in the 4 sets of data below.
1. The personal best (fastest) pitch of the student from Father McGivney is twenty miles an hour faster than that of the student from St. Brother Andre.
2. Muizz's fastest pitch to date is 30 mph faster than that of the pitcher representing Cardinal Carter Academy.
3. Joshua, who represents Sacred Heart, has a personal fastest pitch which is 10 mph faster than that of the student representing St. Jean de Brebeuf.
4. Siddharth's personal fastest pitch is either 20 or 30 mph faster than Dimitrios's personal fastest pitch.
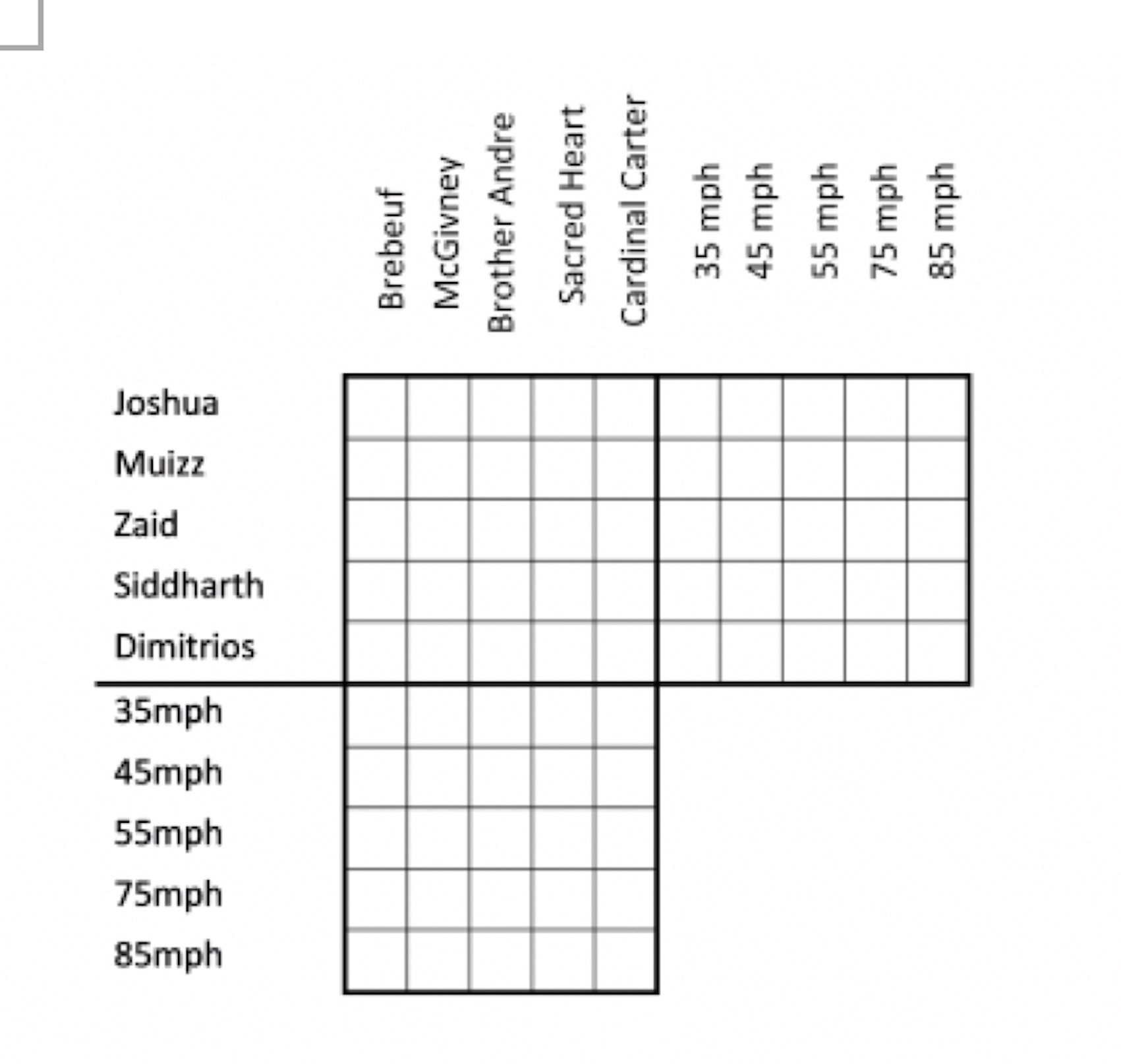
All we need to do at this point is draw out the logical implications of the information provided; doing so will make explicit data that is implicit. We can then proceed to eliminate possibilities inconsistent with the available data and eventually fit every piece of data into its proper place. Because this procedure is a matter of educing what is already contained in the information provided, this puzzle is a matter of deduction.
We begin by eliminating alternatives that prove to be impossible, given the data. For example, the student from Father McGivney could not be the one with the 35 mph fastball, because his pitch is faster than at least one of the remaining four, and 35 mph is the slowest pitch (so we can place an X in the 35 mph row/McGivney column). We also know that the student from Brother Andre does not have the fastest pitch (85 mph) because his pitch is 20 mph slower than the student from McGivney (so we can place an X in the 85 mph row/Brother Andre column). Given that information, we know that if his pitch were 45 mph, then the student from McGivney would have a 65 mph fastball, but no one has a 65 mph fastball, so the Brother Andre student does not have a 45 mph fastball (and we place the X accordingly).
On the basis of information provided by the second set, we know that Muizz is not the student with the 35 mph fastball, and that the Cardinal Carter student is not the one with the 85 mph fastball-for no one is faster than the one with the 85 mph fastball. The student from Cardinal Carter is not possibly the one with a 35 mph fastball, because that would make Muizz's pitch 65 mph, and 65 mph is not an available alternative. The Cardinal Carter student is not the one with the 75 mph fastball, for that would place Muizz's pitch at 95 mph, and that too is not an available alternative.
On the basis of the data in the third set, we know that Joshua is the student representing Sacred Heart. Joshua pitches 10 mph faster than the student representing Brebeuf. That means the student from Brebeuf is not the fastest pitcher. But it does mean that the Brebeuf pitcher is only 10 mph behind Joshua. We're already ruled out that Brebeuf is the 35 mph pitcher, and we've ruled out that Brebeuf is the 45 mph pitcher. Brebeuf could not be the 55 mph pitcher, because that would make Joshua a 65 mph pitcher, and 65 mph is not an alternative. That means Brebeuf is the 75 mph pitcher, and Joshua is the 85 mph pitcher, and Joshua represents Sacred Heart.
On the basis of the information contained in the fourth set of data, we know that Siddharth is not the slowest pitcher and Dimitrios is not the fastest. Dimitrios's fastest pitch is either 20 or 30 mph slower than Siddharth's. That means that if Dimitrios was the slowest pitcher (35 mph), Siddharth would be pitching at a speed of at least 55mph. So clearly Siddharth is not the pitcher with the 45 mph fastball. We know that Dimitrios could not be the pitcher with the 75 mph fastball; for that would make Siddharth a 95 or 105 mph pitcher, and those are not available alternatives. Besides, Joshua has already been determined to be the fastest pitcher. So, Dimitrios is either the 35, 45, or 55 mph pitcher.
We know, looking at all the information we now have, that Dimitrios is not from Brebeuf (who has the 75 mph fastball).
The one with the 35 mph is from Brother Andre. We know that Muizz is not from Brother Andre, and Siddharth is not from Brother Andre.
We know the 45 mph pitcher is from Cardinal Carter, and that means the pitcher from McGivney is the 55 mph pitcher.
Going back to the second set of information, we know that Muizz is the 75 mph pitcher, because he is 30 mph faster than Cardinal Carter, who has the 45 mph fastball. Returning to the third set of data, we know that the 75 mph pitcher is from Brebeuf; hence, Muizz is from Brebeuf.
We now know that Siddharth is the 55 mph pitcher, and so Siddharth is the McGivney student. Returning to the fourth set of data, we know that Siddharth's pitch is 20 or 30 mph faster than Dimitrios's, and so Dimitrios is the slowest pitcher at 35 mph (not 45 mph). That leave Zaid as the 45 mph pitcher. Hence, Zaid is from Cardinal Carter. Finally, Dimitrios is the Brother Andre student.
Article copyrights are held solely by author.
[ Japan-Lifeissues.net ] [ OMI Japan/Korea ]